前面一篇文章讲解过BFS和DFS的基本概念常见用法,今天专注于图论中的BFS,来深入的探讨一下BFS在图论的搜索中的应用,并总结相关解题技巧。
本文假定已经熟知图论的基本知识,比如图的表示方式和一些基本概念等,如不熟悉可以参考此文。
基础(单源)BFS
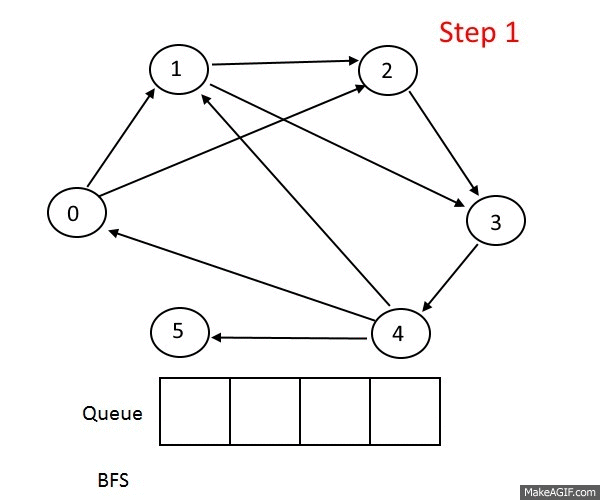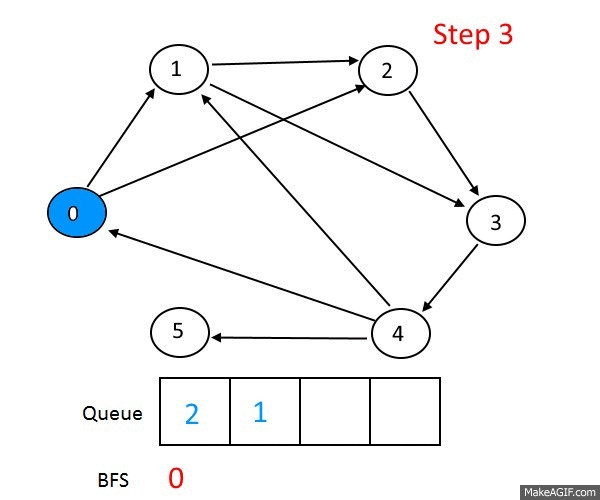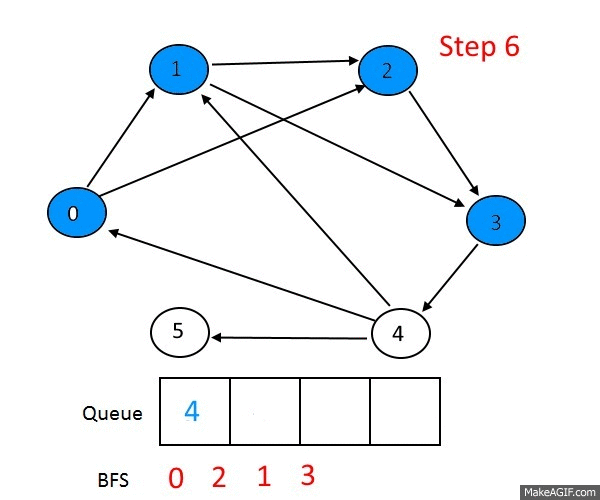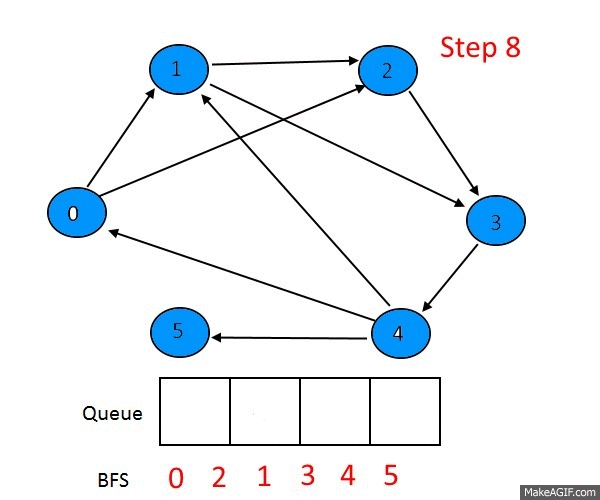
基础的BFS通常是单源的,也就是以某一个顶点为起点。借助队列(FIFO先入先出队列),把起点入队,然后不断的从队出取出顶点,访问与其连通的顶点,直到队列为空。为了防止重复遍历,需要在遍历过程中做标记。因为这个比较基础,我们在前一篇文章中已有伪码,所以这里就不再重复了。
这是最基础的BFS,当然 也是最重要的,因为更为复杂的玩法也是基于此的,因此要烂熟于心,有一些板子题,可以时常拿出来复习一下:
| 题目 | 题解 | 说明 |
|---|---|---|
| 200. 岛屿数量 | 题解 | 邻接矩阵,矩阵式基础BFS板子题 |
| 695. 岛屿的最大面积 | 题解 | 邻接矩阵,矩阵式基础BFS板子题 |
| 733. 图像渲染 | 题解 | 邻接矩阵,矩阵式基础BFS板子题 |
| 1905. 统计子岛屿 | 题解 | 邻接矩阵,矩阵式基础BFS板子题 |
| 1466. 重新规划路线 | 题解 | |
| 841. 钥匙和房间 | 题解 | |
| 题解 | ||
| 题解 |
多方向邻接
对于矩阵来说一般的邻接是四个方向,上下左右,但有时斜角也算邻接,这就有了八个方向,整体遍历的套路不变,只不过在找邻接顶点时要考虑八个方向。
| 题目 | 题解 | 说明 |
|---|---|---|
| 1091. 二进制矩阵中的最短路径 | 题解 | |
| 面试题 16.19. 水域大小 | 题解 | |
| 题解 |
二分图判定之着色法BFS
先要讲下二分图的定义:对于图中的任意两顶点u和v,如果它们有一条边直接相连,那么u和v必须属于不同的集合。更为学术一点的说法是:如果能将一个图的顶点集合分割为两个独立的子集A和B,并使略中的每一条边的两个节点一个来自于A集合,一个来自于B集合,就将这个图称为二分图。
有些题目,并不会这么直接的告诉你这是一个判定二分图,而且会做一些信息隐藏,一般而言,如果 涉及把一个图的顶点进行归类,只分为两类,并且有边直连的顶点要归在不同的类别中,那么这就是一个二分图判定问题,比如题886,给你的是某人不喜欢的一群人,显然有边连接的顶点要归属于不同的集合,那么这就是一个二分图判定题。
可以用着色法BFS来判定二分图,大概的算法流程如下:
- 用一个与顶点集合一样大的整数数组(或者其他结构)用作颜色标记,0是未着色(也就是还未访问),1着成红色,2着成绿色
- 任选一个顶点作为起点,着色为1(红色),加入队列,开始BFS
- 当队列不为空时,取出当前顶点u,遍历与u直连的顶点v,如果v还未着色,则把它加入队列,并着为3-color[u];如果v已着色,且与color[u]着色一样,则说明不是二分图,返回F并终止遍历;
- 重复3直到队列为空,说明可以把所有顶点着为不同的色,也即是二分图,返回T
伪码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 | |
| 题目 | 题解 | 说明 |
|---|---|---|
| 785. 判断二分图 | 题解 | 二分图判定板子题 |
| 886. 可能的二分法 | 题解 | 二分图判定模板题 |
| 题解 |
注意:二分图是把图的顶点进行分类到不同的集合,这是并查集最为擅长的应用场景,因此用并查集解决二分图判定更为高效和优雅。关于并查集可以参考此文。
多源BFS
基础的BFS只有一个起点,把图中的某一个顶点最先放入队列,然后开始BFS。但有些场景,以单个顶点为起点不能解决问题。这类问题的特点一般是求某一类顶点的极值,比如0-1矩阵中,求0最近的1,或者求1最近的0。这里的要点在于说单个顶点通过BFS找到的值并不一定是全局最优解。而如果以每个顶点都做一遍BFS又会导致复杂度太高,不但复杂度超高,而且有时候会难以编码(大致的思路是有的,但难以转化为具体的代码)。这时就要用到更为复杂一些的多源BFS来求解。
需要应用多源BFS题目的特点是与多个顶点相关,并求一个全局最优解,也就是说求顶点集合到另一个顶点集合的距离或者路径长度。有时候我们还需要运用逆向思维,反向思考,以使问题简化,比如虽然题目求0到1的距离,但如果反着去计算1到0的距离,反倒更为方便一些,那么就需要把顶点集合反一下。
多源BFS的套路:
- 依据题目信息,看是否要把顶点集互换一下,大部分的题目是需要互换的
- 把点集都加入到队列中,同时入队的还有一个初始状态,比如求最短路径,可以把MAX_INTEGER加进去
- 以这些点集为起始,去做BFS,同时更新状态,这与常规BFS就一样了
- 为了防止重复遍历也是要做标记的,这与常规BFS一样,可以用步骤3里面与顶点一起入队的状态来当作标记,比如是MAX_INTEGER时肯定是还未访问到,是其他值时说明已访问过了
- 遍历过程中,可以求得全局最优解
| 题目 | 题解 | 说明 |
|---|---|---|
| 542. 01 矩阵 | 题解 | 点集互换,多源BFS模板题,多源最短路径 |
| 934. 最短的桥 | 题解 | 多源BFS,数圈圈 |
| 994. 腐烂的橘子 | 题解 | 多源BFS |
| 1162. 地图分析 | 题解 | 点集互换,多源最短路径 |
| 1129. 颜色交替的最短路径 | 题解 | 双源BFS |
圈式BFS
单源多源都可以,重点不是起点的多少,而是要在遍历的时候注意数圈层。BFS的特点是像水波一样一层一层,一圈一圈的由起点向外传播,有时候我们需要对这些层和圈进行计数。
其实,这个跟树的层序遍历是一样的,树的遍历大法可以参考 这个文章,如果对树的层序遍历熟悉了,那么图的数圈圈也就会了。做法就是添加下一层时做一下标记,就可以了,并不复杂。
| 题目 | 题解 | 说明 |
|---|---|---|
| 909. 蛇梯棋 | 题解 | 因为可能往回走,格子数据不能被覆盖,必须用额外空间当标记,不可以原地标记。 |
| 934. 最短的桥 | 题解 | 多源BFS,数圈圈 |
| 题解 | ||
| 题解 |
泛图BFS(枚举)
图是一个很广泛的概念,任何事情都可以视为一个顶点,事物之间的联系可视一条边,状态也可以视为一个顶点,一个状态变化 为另一个状态可视为一条边,因此图论的搜索,或者说图论的遍历方式可以广泛的应用。
BFS的遍历特点是能找到两个顶点之间的最短路径,因此,当找一些状态与状态之间的最少变化次数之类的问题时,经过适当的建模后,便可以用图论的BFS来求解。
针对广泛图应用BFS的套路:
- 针对 状态进行建模,确定状态的变化规律
- 搞清楚状态的变化 规律后就可以建图了,要注意图是否是无限图,如果是无限图就必须找遍历搜索的边界
- 把起点加入队列,确定标记方案,然后开始做BFS
- 注意边界,包括重复标记,以及搜索的边界,以防止进入死循环
| 题目 | 题解 | 说明 |
|---|---|---|
| 1306. 跳跃游戏 III | 题解 | 模板题,本身是数组边界固定 |
| 1654. 到家的最少跳跃次数 | 题解 | 容易想到BFS,确定右界是关键 |
| 433. 最小基因变化 | 题解 | 枚举状态的模板题 |
| 752. 打开转盘锁 | 题解 | 枚举状态的模板题 |
| 365. 水壶问题 | 题解 | 建模定义状态,转换状态 |
| 题解 | ||
| 题解 |
注意:本质上,这属于枚举,我们枚举各种状态,然后找到想要的答案。用BFS来枚举是寻找两种状态之间的最少变化 次数。而DFS枚举则用于查找所有的可行方案,这其实就是回溯算法了。图论真的博大精深,与各种算法融合在一起。
复杂状态处理
图的遍历可复杂也可简单,重点并不是遍历方式如DFS,单源BFS或者多源BFS,而且遍历到每个节点时,对节点状态的处理,这里可能会千变万化,有些难题就难在对状态的处理,有些是状态太复杂了,要想办法压缩 以达到可处理的地步(如题847),有些则是状态变化 太多了(如题417)。这有点类似于动态规划,是没有固定的套路的,只能靠平时积累以及分析建模能力了。
| 题目 | 题解 | 说明 |
|---|---|---|
| 847. 访问所有节点的最短路径 | 题解 | 多源BFS,状态压缩 |
| 864. 获取所有钥匙的最短路径 | 题解 | 状态压缩 |
| 1926. 迷宫中离入口最近的出口 | 题解 | 单源最短路 |
| 题解 | ||
| 题解 | ||
| 题解 |
双向BFS
无论是单源还是多源做BFS时一般都是一个方向的,也就是说把起始顶点或者点集加入队列作为起点,向着目标顶点或者点集或者说终点去BFS遍历。通常情况下,这没什么问题。
但当数据量特别大时,或者状态的计算比较复杂时,这样效率就不够高了,这时需要更为复杂的玩法。其实前面说的起点和终点都是相对的,图的搜索遍历其实是不分方向的,起点到终点的最短距离,与终点到起点的最短距离其实是一样的,反过来你把终点当成起点来做BFS也是一样的(前面讲多源BFS时就提到过逆向思维,把点集对换,其实就是从原终点当作新起点做BFS)。
那么,假如同时从起点开始,和从终点开始一起做BFS,当两个BFS相遇时(同时到达相同的一层顶点时)搜索完成,是不是搜索效率就会加倍?这就是双向BFS的核心思想。另外,为了保证平衡性和效率,每次要优先把队列元素数量小的一个方向向前推进。
| 题目 | 题解 | 说明 |
|---|---|---|
| 126. 单词接龙 II | 题解 | |
| 127. 单词接龙 | 题解 | |
| 1091. 二进制矩阵中的最短路径 | 题解 | |
| 题解 | ||
| 题解 |
逆向遍历
图的遍历都是从某些顶点出发,去寻找另外的顶点。有些时候是起始顶点已知,比如前面提到的常规遍历问题,无论是单源还是多源,都是起点是已知的固定的一个顶点集合。
但有时候,起点并不固定,但终点是固定的,这时候就需要运用逆向思维,从这些固定的终点出发做遍历,进而求解。
| 题目 | 题解 | 说明 |
|---|---|---|
| 417. 太平洋大西洋水流问题 | 题解 | 典型的终点固定,起点不固定,从终点出发遍历 |
| 题解 | ||
| 题解 | ||
| 题解 |
拓朴排序
对于有向无环图而言,拓朴排序能够把顶点按依赖顺序排成线性列表,用的也是BFS来实现的,详情可以参考此文。