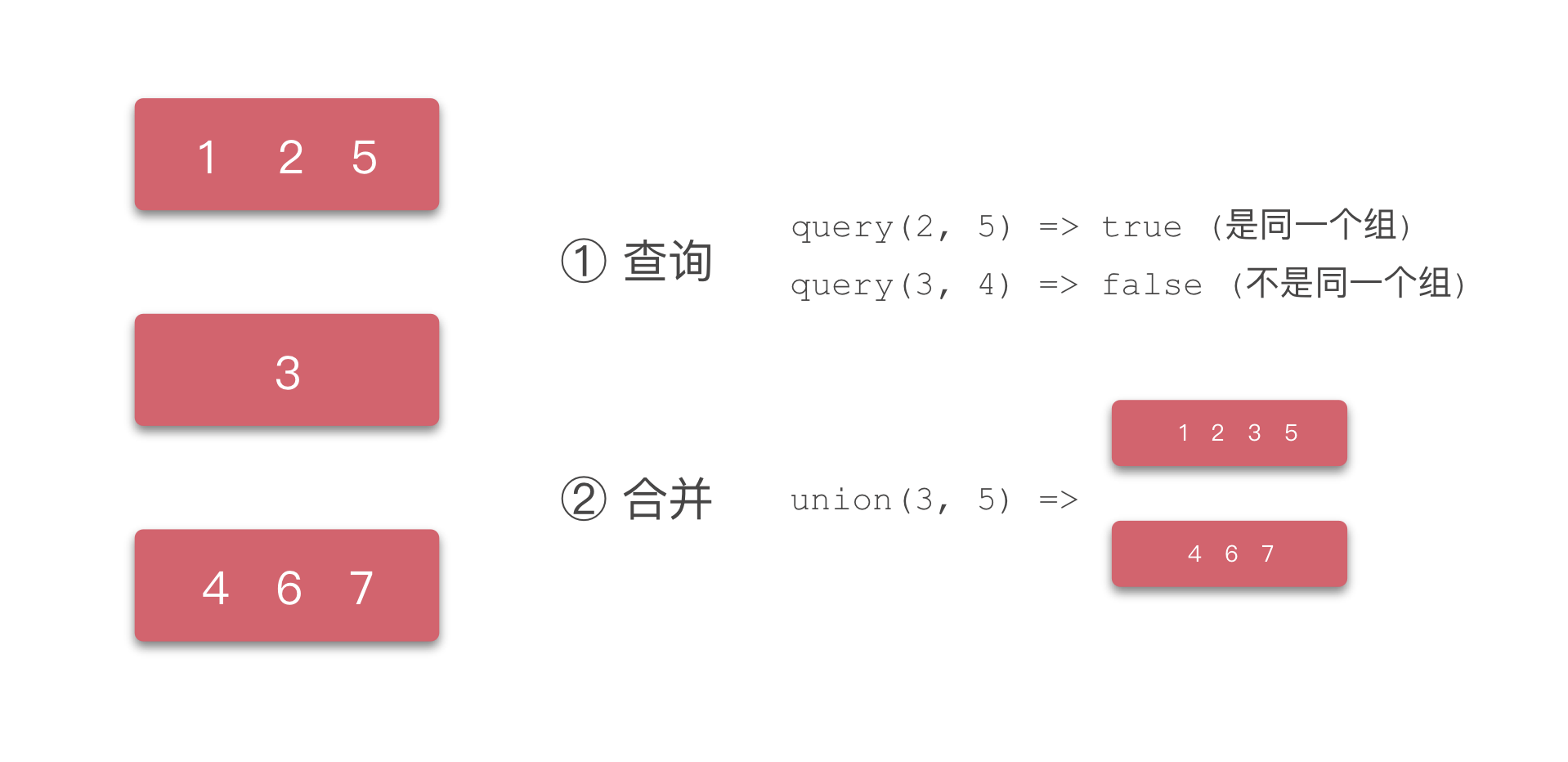
并查集（Disjoint-set Data Structure）是一种树形的结构，用于处理不相交的集合的高效的查询(find)和合并(union)问题。主要有两种操作一是查询(find)，也就是查询某个元素是否属于某个集合；二是合并(union)，也即把某个加入到某个集合中，这里的集合都是无交集的。通过路径压缩，并查集的查询和合并都可以达到常数级别O(1)。

朋友关系问题

先来看一个问题，比如有一个朋友关系的问题，两个人可以成为朋友关系，两两是朋友的一群人就形成了一个朋友圈，那么如何快速判断某两个是不是朋友关系呢？又如何让两个人成为朋友呢？

一个可行的方法是用图的搜索，两个人的朋友关系可以视为图的一条边，一个朋友圈就是相互连通的一个图，查看两人是否是朋友关系，可以从一个人出发，不断遍历相连的边，看能否到达另一个人，但这样效率有点低，每次查询 都会是线性时间，因为都要遍历一遍图才知道。

我们换个思路，可以为一个朋友图指定一个『圈长』，把关系改成其他人都直接跟圈长相连，或者每个人都能找到自己的圈长，这时判断两个人是不是在同一个朋友圈内，就看它们的圈长是不是同一个人就可以了，这就是并查集。

并查集的概念与基本实现

并查集用以表示不相交的集合，逻辑上它是一种扁平的树形结构，每一个树代表一个集合，树的根就是这个集合的『圈长』，或者叫做一个集合的代表（representative）。并查集支持两种操作，查询（find） 和合并（union），查询是看两个元素是否属于同一个集合，合并则是把两个集合合并成为一个集合。

并查集的精髓就在于它的『圈长』机制，我们不管具体某个元素它的路径与关系，每个元素都只关心自己的圈长，它能找到自己的圈长就可以，因此查询是否属于同一个集合就看元素的圈长是否是同一个；合并，也非常简单，两个集合合并，就是把其中一个圈长的圈长设置为另一个圈长就可以了。

具体实现

需要注意，虽然并查集逻辑上是一种树形结构，但一般情况都用线性的数组来实现并查集。比如用一个长度为n的数组来表示并查集，实际上我们只关心圈长，所以下标为i的元素就是i的圈长，一般命名为parent，也就是说parent[i]就是i的圈长，或者顺着它就能找到圈长（树的根），而parent[i]=i则是一个集合的『圈长』（representative）。

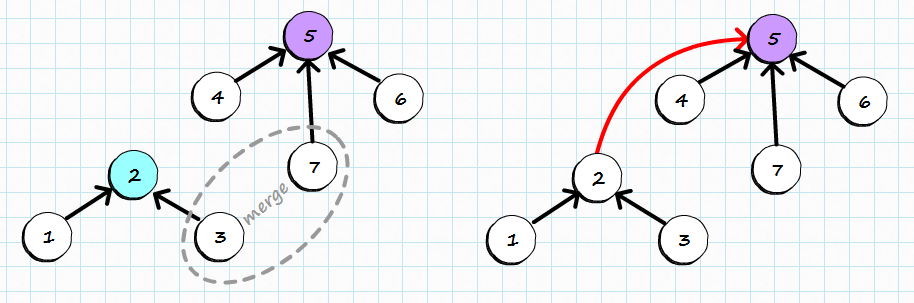
初始时，每个元素都是独立的，每个元素都独立成团，自己就是圈长，也即parent[i]=i。当有元素合并了，就把它们指向同一个圈长，比如parent[8]=6，parent[1]=6，parent[2]=4，parent[3]=4，parent[9]=4，parent[7]=4，这样就知道一共有三个集合，其中5独自成一个集合，1和8还有6是同一个集合6是他们的圈长，2，3，9，7，4是同一个集合4是圈长，画出图来就是这样的：

查询与合并

查询某两个元素是否属于同一个集合，就是归结来查找每个人所属集合的圈长（representative），然后判断是否是同一个元素，因此问题归结为圈长的查找。比如2的父节点是4，而parent[4]=4，它就是圈长，所以2的圈长是4；再看7，它的父节点是9，而9的父节点是4，4是圈长，因此2和7属于同一个集合。

合并，也是类似的，而且更加简单，先查询要合并是否属于同一个集合，如果属于那自然就不用合并了。如果不是，那就找到各自的圈长，然后把某一个圈长的圈长设为另一个即可。比如想把5和8合并，5独自成圈，而8的圈长是6，那么把5的圈长设置为6，parent[5]=6，就合并完成了。

注意：并查集的具体实现要看实际数据类型，比如集合元素个休是一个0~n范围内的整数，那么自然用数据非常方便，或者能够方便的转化为数组的下标时，用数组也行。否则也可以用哈希表。因为元素只要能递归的向上找到它的圈长（树的根）就行。

路径压缩

从前面的例子来看，查询过程其实是O(n)的，因为某个元素的父节点不一定就是圈长，为了找到圈长要递归的找下去，直到找到圈长为止，即只有找到了parent[i]=i，才算找到了圈长。这样每次查询都是线性时间，就会导致并查集整体效率变成O(n²)的。

因为并查集是处理集合问题，也就是说我们只关系某两个元素是否属于同一个集合，至于它跟其他元素之间的关系并不重要，我们只希望快速的找到它的圈长就可以了，那么我们在查找圈长的过程中，就可以把元素都直接指向其圈长，比如前面的7，它的父节点是9，不是圈长，我们查找后发现圈长是4，那么在查询过程中就可以把parent[7]=4，让7的父节点变成圈长。这样做的好处是，下次再查询时就能直接找到圈长了，变成了O(1)，不用再线性去查找了，这便是路径压缩。路径压缩的复杂度是常数级别的。准确说它的复杂度是O(alpha(n))，这个alpha(n)叫做反阿克曼函数，当n无限增大时，这个函数的极限值是5，有兴趣的可以深入研究。

最终树变成了扁平的，集合中的每一个元素都直接指向圈长：

按秩合并

合并的时候是把一个集合的圈长的圈长设置为另一个集合的圈长，比如前面5和8要合并，5的圈长是5，8的圈长是6，这时其实有两种可行方法，可以把5的圈长设为6，即parent[5]=6，但也可以把6的圈长设置为5啊，即parent[6]=5，逻辑上都可行的，但应该用哪种呢？

逻辑上并无对错，要从效率上来比较哪个更好。前面提到了，常规查询是线性时间的，集合是树形的，树的高度越高，那么找到圈长的时间就越长，路径压缩后树才会变得扁平，因此，可以认为树的高度是越小越好的。由此来看，把5的圈长设置为6效率更高，6这个集合高度是2，如果把6的圈长设置为5，那么树的高度会变成3，需要一次路径压缩才可以；相反，如果把5的圈长设置为6，即parent[5]=6，那么树的高度还是2，不需要额外的路径压缩了。所以应该把高度小的集合并到高度大的集合中去。

那么，可以用另外一个数组rank来表示集合的秩，即rank[i]是i所属于集合的秩，也就是树的高度，当合并的时候就可以参考 rank来进行更高效的合并，总是把秩低的往秩高的上面的合并。只看圈长的秩就可以了，因为合并的时候是两个圈长在打架。

实例

还是来一个具体的实例，来演示并查集的思路和具体实现。把朋友圈关系进行抽象，用数字0~n来代表N个人，N=n+1，实现一个并查集，并进行查询和合并操作。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60

public class DisjointSet {
    private int size;
    private int[] parent;
    private int[] rank;

    public DisjointSet(int size) {
        this.size = size;
        parent = new int[size];
        rank = new int[size];
        init();
    }

    private void init() {
        for (int i = 0; i < size; i++) {
            parent[i] = i;
        }
    }

    public void union(int x, int y) {
        int xRoot = find(x);
        int yRoot = find(y);

        if (xRoot == yRoot) {
            // In the same set already, do nothing
            return;
        }

        // Union by rank, ruled by higher rank.
        if (rank[xRoot] < rank[yRoot]) {
            parent[xRoot] = yRoot;
        } else if (rank[xRoot] > rank[yRoot]) {
            parent[yRoot] = xRoot;
        } else {
            parent[xRoot] = yRoot;
            rank[yRoot]++;
        }
    }

    public int find(int x) {
        if (parent[x] == x) {
            return x;
        }

        // Path compression
        int root = find(parent[x]);
        // Make each node point to its root
        parent[x] = root;
        return root;
    }

    public static void main(String[] args) {
        DisjointSet dset = new DisjointSet(5);
        dset.union(0, 2);
        dset.union(4, 2);
        dset.union(1, 3);

        System.out.println("True: " + (dset.find(4) == dset.find(0)));
        System.out.println("False: " + (dset.find(1) == dset.find(0)));
    }
}

并查集的应用

可以发现并查集是一个很优雅的数据结构，它的实现很简单，效率却非常高。凡是涉及不相交集合的查找与合并问题，都可以使用并查集来解决问题。这里最为关键的是集合元素之间不能有交集，也就是说除以我们指定的圈长方式来划分集合以外，不能有其他的约束条件，否则并查集就失效了。比如说现实生活中的人，可以以工作所在的公司来划分集合，也可以以住的小区来划分，假如题目中两个约束条件都在，那就没有办法应用并查集了。

并查集相关的题目，一般求解的是集合的数量，或者找最大集合，或者找最小集合。这两种统计结果都可以由内部的数据来得到。比如集合的数量，就是遍历parent数组，找到所有的parent[i]=i；而集合的大小，则可以用用秩来追踪，只需要合并的时候把秩也加上，最大集合就是找秩的最大值，可以参考题695。

并查集最大的特点是集合中的元素直接跟根节点产生关系，因此如果能够根据元素与根节点的关系继而计算出两两元素之间的关系，那么也是可以应用并查集的，带权并查集就是此类问题，可参考 题399。

典型题目

参考资料

• Disjoint Set Data Structures
• Disjoint Set Union
• Disjoint set data structure
• Disjoint–Set Data Structure (Union–Find Algorithm)
• Disjoint Set Union (Union Find)
• 算法学习笔记(1) : 并查集
• 并查集
• 并查集算法
• 图解并查集，附赠几道 Leetcode 练手题
• 简单并查集讲解（并+查）与代码实现
• 并查集
• 并查集从入门到出门