图（Graph)）是一个由节点和边组成的略复杂的二维数据结构，通常用于表示物体之间的关系。
图的基础知识
图由节点（Vertex）和边（Edge）组成，节点之间会有边来连接以表示某种关系。逻辑上的形状会是这样子的：
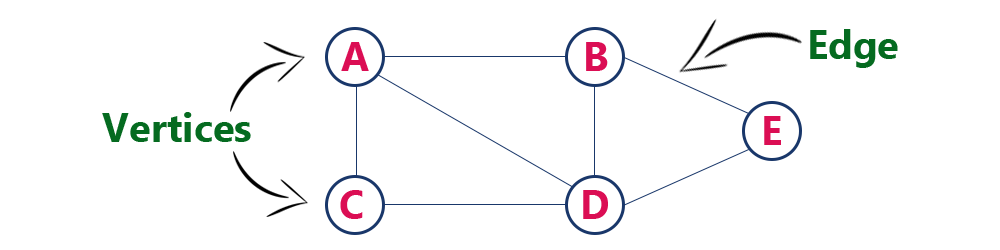
图的节点通常用于表示物体或者数值，变化较少，图的复杂性主要就体现在边上面，比如有些是有向的，有些是无向的，还有指向自己的。
顶点
顶点即Vertex，是图的基本单元，也称作节点。
边
边是Edge，两个顶点之间的连接称为边。分为无方向的，有方向的，和带权重的。
权重
权重，weight，是边的一个属性，一条边（也即两个顶点的连接）可以带有权重以表示某种成本。
路径 Path
在一个图中，路径是一系列节点和边，其中的节点都由边连接
路径长度 Path length
两个节点之间的边的数量称为路径长度
简单路径 Simple Path
一个路径所经过的节点没有重复的，就称为简单路径
根 Root
如果一个节点，由它出发的路径可以连通到所有节点，那么这个节点称作图根
环 Cycle
存在路径起始节点相同，就形成了环
度 Degrees
针对 节点而言，经过一个节点的所有边的数量之和，称之为节点的度
入度 In degress
对于有向图而言，以节点为终点的边的数量，称这节点的入度。
出度 Out degrees
对于有向图而言，从一个节点出发的边的数量，称为节点的出度。
图的分类
空图 Null graph
也就是只有顶点，没有边的图，样子大概是这样：
有限图 Finite graph
顶点和边的数量是有限的，接触到的绝大多数图都是有限图。
无限图 Infinite graph
顶点和边的数量是无限的
完全图 Complete graph
所有节点都是有路径连通的
权重图 Weighted graph
每一条边都有一个数值表示的权重以代表两个节点之间的某种成本
无向图 Undirected graph
连接节点之间的边是没有方向的，称之为无向图，它也是普通 的图
有向图 Directed graph
每条边都是有方向的，对于两个节点来说v[i]和v[j]来说，e[i,j]=(v[i],v[j])，它与e[j,i]=(v[j],v[i])是不一样的，有向图通常用于表示物体之间的依赖关系
连通图 Connected graph
任意两节点都连通，称之为连通图也叫强连通图。
非连通图 Disconnected graph
有两个节点没有边连接，就称为非连通图。
自环
也就是某个节点有一条边是自己连接着自己，这个有向和无向图都可以有
有环图 Cyclic graph
起点和终点相同的路径，就形成了环。如果图中存在一个环，就是有环图。
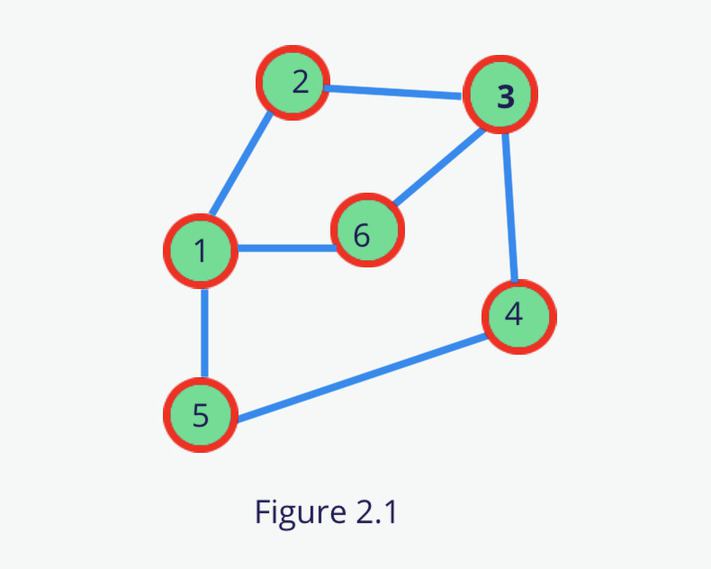
无环图 Acyclic graph
图中没有环就是无环图
有向无环图 Directed Acyclic Graph
有向图中不存在环就是DAG，这是比较重要的一种图，拓扑排序 可以验证DAG。
图的表示方法
图的表示方法一般有邻接矩阵法和邻接表法。
邻接矩阵 Adjacency Matrix
对于有n个顶点的图来说要创建一个nxn的矩阵来表示此图，每一个格子[i,j]表示顶点v[i]到v[j]是连通的，有一条边存在，如果是有向图，则[j,i]表示v[j]到v[i]的边。另外，如果有权重，格子的值也可以表示边的权重。
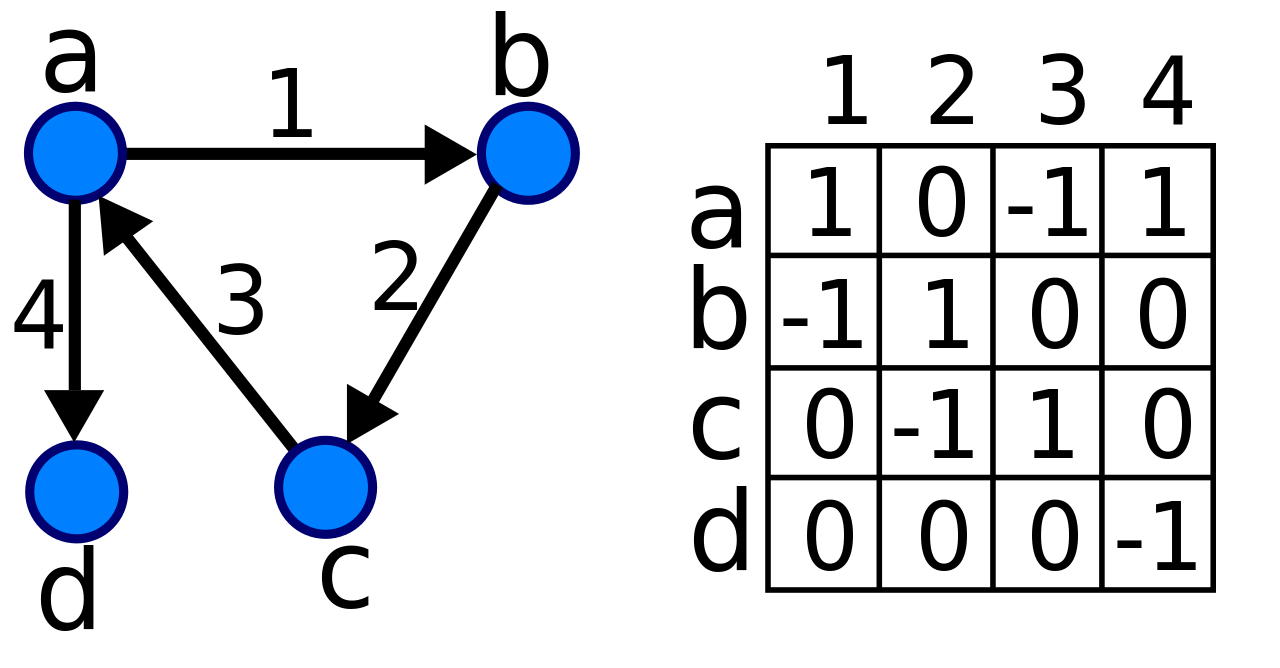因为用矩阵一般比较浪费空间，比如顶点较多，但边较少时，就有点浪费空间。一般，矩阵通常就是一类单独的矩阵类搜索问题，直接应用图的搜索方法。
邻接表 Adjacency List
也就是列表的列表，先用一个链表代表所有的顶点，然后这个链表的元素是这个与这个顶点相连的所有顶点组成的列表。
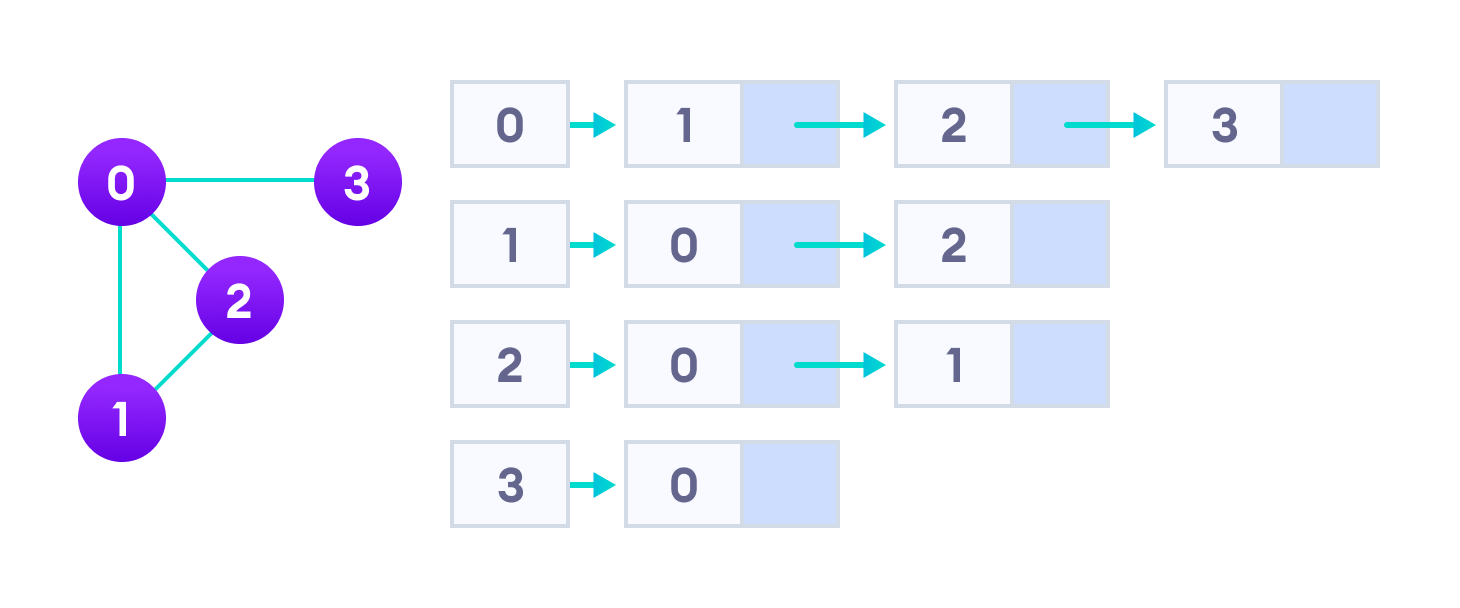通常是用数组加链表的形式，主表用数组或者可变长数组，因为这些都是顶点，有可能会随时从某个顶点开始遍历，所以要用随机访问效率高一些的数组。与顶点相连的顶点列表一般用链表，因为它方便删除和插入，且遍历一般都是从顶点开始遍历。
但，也要看实际情况，有时候用哈希表也可以，键是每个顶点，值为顶点所连接的顶点列表，顶点列表可以用列表，也可以用Set等等。
邻接表的实现方式比较自由，只要能从一个顶点出发，方便的找到与其相连的顶点，就可以。具体的，可以依据实际数据情况来灵活选择，比如说顶点如果是某一个范围内的整数，那么可能用数组就更方便一些，如果是字串或者其他的，可能用哈希表就更方便一些。
图与树的关系
图是一个比较大的概念，只要是有节点与节点相连接就可以看作是图，数组（可视为下标与元素的连接），哈希表（键与值的连接），树，链表都可以看作是图。这些数据结构是一种特殊的图，强加了很多其他规则，就比如树，有一个根，有多个子节点。
适用于图的很多算法也适用树，比如DFS和BFS对树也是适用的。
求反图
这是针对有向图而言的，如果把有向图的每条边都方向反一下，比如原来是e: u -> v，改为e’: v -> u，得到的就是原图的反图。求反图有时候能够帮助打开思路，突破局限，使原先一些无法下手的题目，找到已有的工具和方法来解决。比如说拓朴排序，是不断的找入度为0的顶点，有些顶点则是终端顶点，也就是出度为0，但出度为0没啥特质，也没有对应的工具和方法来做处理，但如果把图反一下，出度为0的顶点，反了后就是入度为0的顶点了，这时就可以应用拓朴排序了，比如题802就是先求反图的典型例子。
典型题目
| 题目 | 题解 | 说明 |
|---|---|---|
| 802. 找到最终的安全状态 | 题解 | 先求反图，再拓朴排序 |
| 997. 找到小镇的法官 | 题解 | 入度与出度 |
| 1557. 可以到达所有点的最少点数目 | 题解 | 入度与出度 |
| 1615. 最大网络秩 | 题解 | 度 |
| 1791. 找出星型图的中心节点 | 题解 | 度 |
| 题解 |