有过Android开发经验的小伙伴对startActivityForResult)以及onActivityResult)一定不陌生,正是这一对API让组件 的复用变成可能。今天就来学习一下如何在函数式的范式中驾驭Activity的跳转。
喜迎国庆,用Compose赶制一面五星红旗
搞定在Jetpack Compose中优雅地申请运行时权限
轻松解决Jetpack Compose中的一些痛点问题
暑去秋来,金桂飘香,不知不觉中我们已经练完了『降Compose十八掌』,相信通过这一系列文章能够对Jetpack Compose有足够的理解,并能在实际项目中进行运用。今天将继续Compose之旅,总结一下Compose使用过程中经常会遇到的一些痛点问题,并学会如何优雅的解决这些问题。
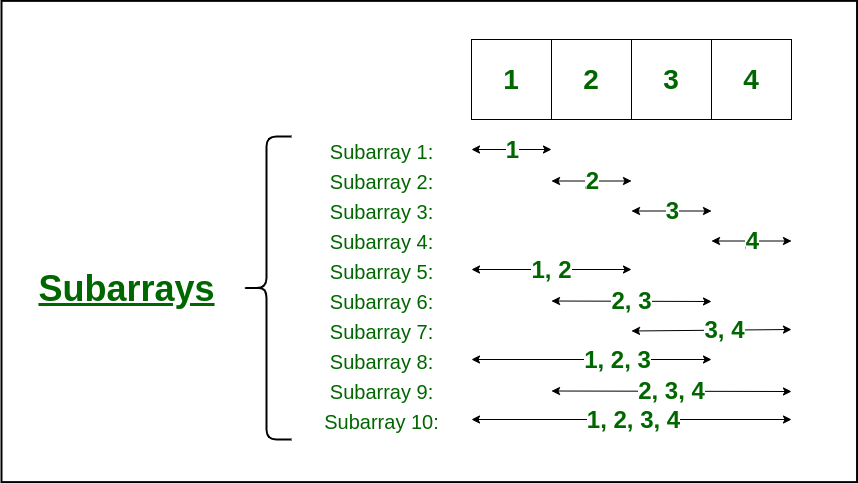
Sub Array and Seb Sequences Made Easy
降Compose十八掌之『神龙摆尾』| Architecture
通过前面的一系列文章,我们已经掌握了足够的Jetpack Compose的开发基础。为了更好的在实际项目中使用Compose,我们还需要了解一下现代应用开发的架构原则,以及使用Jetpack Compose时如何更好的遵循这些原则。这篇文章将聚焦于架构原则这一话题,进行一些探讨和总结。
降Compose十八掌之『羝羊触蕃』| Handle Platform Lifecycles
降Compose十八掌之『履霜冰至』| Phases
这篇文章译自Jetpack Compose phases
就像大多数其他的UI工具集一样,Compose渲染一帧也要经过几个不同的阶段。就比如说Android view系统,主要有三个阶段:测量(measure),版面编排(layout)和绘制(drawing)。Compose也非常的类似,但有一个特别重要的额外的阶段起始时的组合(composition)阶段。
降Compose十八掌之『龙战于野』| Side Effects
主要翻译自官方文档Side-effects in Compose,并不是直译,有些细微调整。
一个副作用是指发生在composable函数范围之外的应用状态的一个变化。由于composable函数的生命周期和诸如不可预测的重组,以不同的顺序执行composable的重组,或者重组可能会被跳过等性质,理论上composable应该要是无副作用的。








:max_bytes\(150000\):strip_icc\(\)/algorithm-df9b57e8ea7c494b891da25987643fab.jpg)