树是非常常见的一种数据结构，有着广泛的应用，而二叉树又是树中最最常见的树，值得好好的学习和总结。 树的定义可以参考这里，二叉树Binary Tree的定义在这里，还有二叉搜索树Binar Search Tree。

二叉树特点

如果节点数量是n，那么高度或者说深度h，那么h至少是logn，最大会是n，节点的位置可以参考 题 655. 输出二叉树 BFS/DFS，这题有树的高度和每个节点的详细信息。

反过来说如果知道树的高度h，那么节点数目至少是h，至多是2^h-1。给定一颗树，求树的深度复杂度是O(logⁿ)。

另外一类问题是，对节点进行编号以方便进行某些计算，这时可以以存在的节点为准而，常见的办法是从父节点往子节点编号，比如父节点编号为i，那么其左子节点就是i*2，而右子节点就是i*2+1。从根节点自上而下，根节点肯定 是0，这样每一层都能从0开始做好编号，且不会重复。如题 662. 二叉树最大宽度

二叉树的特性相关问题

二叉树的常规遍历

二叉树的常规遍历，其实也是深度优先遍历，分为三种先序，中序和后序。这里的所谓的前中后，是指子节点相对于根节点而言的。对于一个最小的二叉树，也就是只有一个左子节点和右子节点的树来说，先序，就是左右子节点在根节点之后，也即根在最前面，中序就是根在左右中间，而后序则是根在最后。以这个『1, 2, 3』为倒的最小树来说，前序即是[1, 2, 3]，中序是[2, 1, 3]而后序 是[2, 3, 1]。

左子节点总是在右子节点前面，左子树总是在右子树前面的，且从整体树来看，遍历的顺序仍旧是从左下到右下，所以需要先找到最左下的一颗最小子树。

递归式

二叉树的递归式遍历，非常的简单，因为非常直观：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

private void preorder(TreeNode root) {
    if (root == null) {
        return;
    }
    System.out.println(root.val);
    preorder(root.left);
    preorder(root.right);
}

private void inorder(TreeNode root) {
    if (root == null) {
        return;
    }
    inorder(root.left);
    System.out.println(root.val);
    inorder(root.right);
}

private void postorder(TreeNode root) {
    if (root == null) {
        return;
    }
    postorder(root.left);
    postorder(root.right);
    System.out.println(root.val);
}

迭代式

迭代式要借助栈，因为要先找到最左下的一颗最小树。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

public List<Integer> preorderTraversal(TreeNode root) {
    List<Integer> result = new LinkedList<>();
    Stack<TreeNode> stack = new Stack<>();
    TreeNode curr = root;
    while (curr != null || !stack.isEmpty()) {
        while (curr != null) {
            result.add(curr.val);
            stack.push(curr);
            curr = curr.left;
        }
        curr = stack.pop();
        curr = curr.right;
    }

    return result;
}

public List<Integer> inorderTraversal(TreeNode root) {
    List<Integer> nodes = new LinkedList<>();
    if (root == null) {
        return nodes;
    }
    Stack<TreeNode> stack = new Stack<>();
    TreeNode curr = root;
    while (curr != null || !stack.isEmpty()) {
        while (curr != null) {
            stack.push(curr);
            curr = curr.left;
        }
        curr = stack.pop();
        nodes.add(curr.val);
        curr = curr.right;
    }

    return nodes;
}

逆序遍历

前面说了，二叉树的常规遍历仍旧是从左下向右下的，如果看成数组，那就相当于是从前往后的。但有些情况吧，逆序遍历会更方便，也跟数组一样，有时候从后向前遍历更为合适。逆序遍历并不难，只需要把左右子树的处理换个位置就行了，先找到最右下的最小子树，从右下往左下走。

把遍历中的左右子节点顺序互换一下后，就是树的逆序遍历了。

典型题目

二叉树的层序遍历

也即是广度优先遍历，但普通的广度优先一般没啥用，实际题目中用的最多是层序遍历。

基础广度优先遍历

借助队列，先把根节点加入队列，利用队列的先进先出特性，从队首取出一个节点，并把它的子节点加入到队尾，直到队列为空为止，这样的遍历顺序 便是 基础的广度优先，但在实际中基本没啥用。

1
2
3
4
5
6
7
8
9
10
11

queue.offer(root);
while (!queue.isEmpty()) {
    TreeNode node = queue.poll();
    System.out.print(node.val);
    if (node.left != null) {
        queue.offer(node.left);
    }
    if (quuee.right != null) {
        queue.offer(node.right);
    }
}

层序遍历

树的特点是一层是父节点，一层是子节点，知道了父节点层，就能找到子节点层，要想对子节点层做操作必须知道其父节点层。因此层序遍历在实际题目中应用很广泛。

如何能知道每一层呢？其实如果能知道一层，就能知道其下一层，它们是递进的关系，也就分开了。幸运的是我们知道第一层（或者说最上面一层）对，它就是根节点，从它开始，就能找出每一层。具体的做法可以用计数法，计算每层的节点数，用以分 开；也可以用双队列法，一层存放父节点，一层存放子节点，然后交换两个列表，个人喜欢使用双队列法。

具体可以参考以下文章，以及题目中的题解都比较详细，就不重复了。

1. 层序遍历 - 介绍
2. 二叉树的层序遍历
3. 迭代+递归 多图演示 102.二叉树的层次遍历

DFS层序遍历

层序遍历本质上也是树的遍历，BFS较为方便进行层序遍历。但DFS也是可以按层来遍历的。DFS的特点是一路向下，先走到一个叶子节点，那么每一层的最左边的节点肯定是最先遍历到的，同时DFS是从根开始向下，所以我们能知道每层的序号，这样用层的序号就可以进行层序遍历。DFS式需要全遍历完了才能把每一层的节点完整的输出来，因此它并不适合真正的层序输出式遍历，因为DFS走完了，才能知道每一层，然后再次遍历一次才能完整的输出所有层。因此DFS式适合计算与层有关的状态，比如层和，层极值等等。

典型题目

路径相关问题

路径定义不尽相同，有些路径是从根节点到叶子的算路径，有些则不必，前面说的都是竖着的路径，也就是从根节点出发到叶子节点，而有些则可以横着的，比如从左子节点经过根节点到右边节点的路径。路径相关的问题很多，且难度上升级一个量级，通常涉及动态规划。

典型问题

二叉搜索树

二叉搜索树Binary Search Tree（常简称作BST），是一种特殊的二叉树，它保证左子树小于根节点小于右子树，如果以中序遍历BST得到的会是一个严格递增的序列。 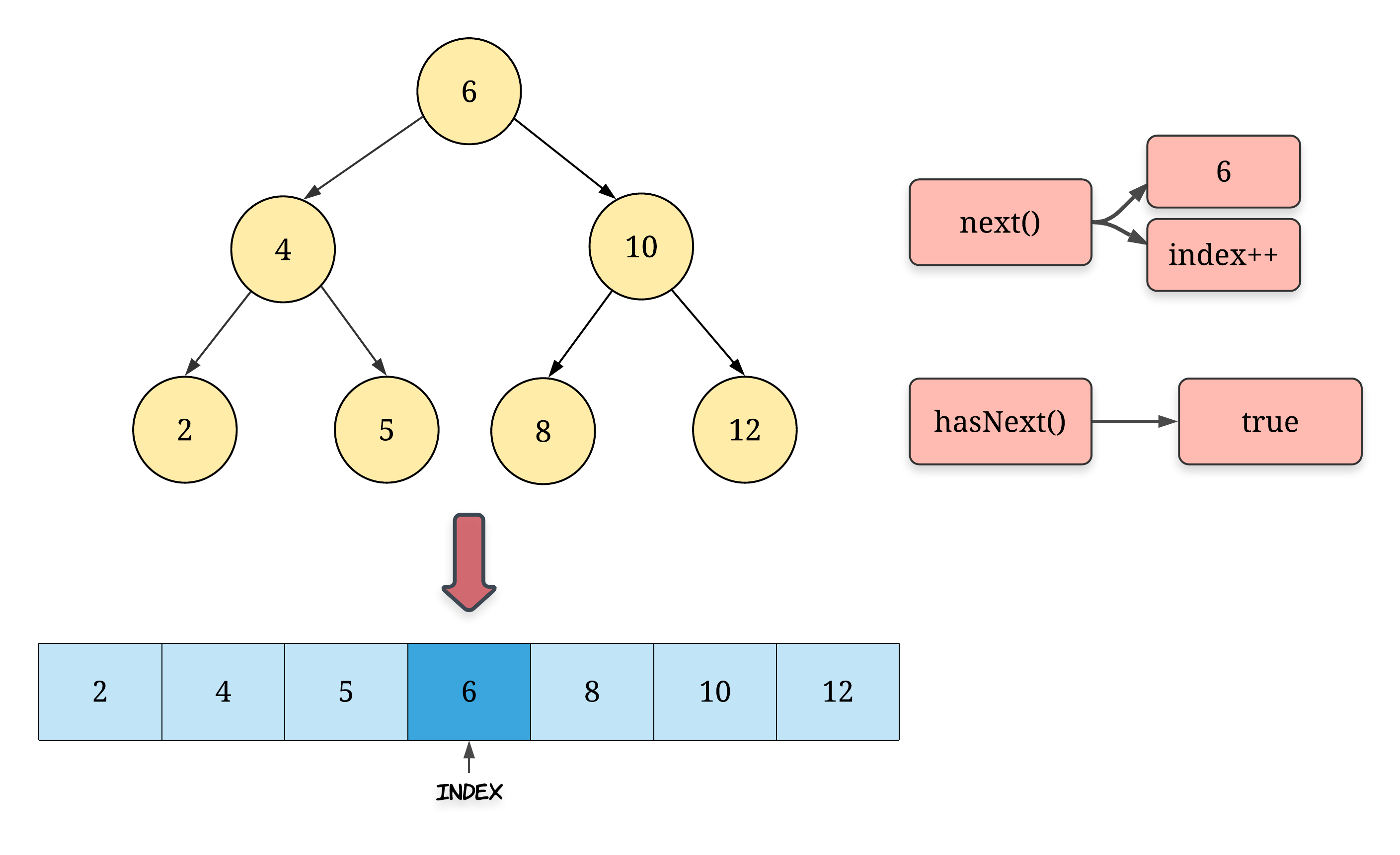BST是一个严格递增的序列，这就是BST的本质，与BST有关的题都要应用二分查找：从根节点开始，目标值等于当前节点值，就找到目标了，小于节点值就向左找，大于就向右找。写成代码就是这样：

1
2
3
4
5
6
7
8
9
10
11

TreeNode node = root;
while (node != null) {
    if (node.val == target) {
        return node;
    } else if (node.val < target) {
        node = node.right;
    } else {
        node = node.left;
    }
}
return null;

这与二分查找是一样的，这就是BST的本质，深刻理解 了它的本质后，一切问题都会迎刃而解。

需要特别注意的是，BST虽然大部分时间的查找都是O(logⁿ)的，但是在极端 情况下，比如树严重的不平衡时，会上升级到接近O(n)水平。因此，当没有特别说明时，或者树的节点特别多时，一定要留心树不平衡的情况，如题2476. 二叉搜索树最近节点查询。

典型题目

参考资料

• 数据结构：树(Tree)【详解】
• 数据结构中”树”的全面讲解
• 数据结构—树（彻底理解递归算法）
• 二叉树的前序遍历
• 二叉树的中序遍历
• 动画演示+三种实现 94. 二叉树的中序遍历
• 二叉树的后序遍历
• 「代码随想录」帮你对二叉树不再迷茫，彻底吃透前中后序递归法（递归三部曲）和迭代法（不统一写法与统一写法）
• 史上最全遍历二叉树详解
• 图解 二叉树的四种遍历