摩尔投票法(Boyer–Moore majority vote algorithm)，也称为『多数投票法』，这个算法解决的问题是：如何在任意多的候选人中，选出获利票数最多的那个。从算法的角度来说就是在一个长度为n的数组中，找出出现次数大于n/2的那个数，称为多数元素或者主要元素(Majority Element)。

理解摩尔投票算法

它的核心思想是让不同的数『相互抵消』，那么剩下的那个数就是Majority Element。要这样来理解，把数组想像成为很多不同颜色的气球，不同颜色的气球相撞就会两两爆破，那么我们让这些不同颜色 的气球两两爆破，最后剩下的那个颜色一定是数量最多的气球。

它分为两个步骤：

1. 相互抵消
2. 验证结果

伪码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

def majorityElement(arr):
   # step 1: kill each other
   major = 0
   vote = 0
   for x in arr:
      if vote > 0 and x != major:
          vote--
      else if vote == 0:
          major = x
          vote++
      else:
          vote++

   # verifty the major element
   count = 0
   for x in arr:
      if x == major:
          count++
   if count > len(arr) / 2:
      return major
   else:
      return None

它的优点在于效率高，能够以O(n)的效率找到数组中的多数元素，并且不占用额外空间。如果能够确定数组中存在多数元素，那么第2步验证过程可以省略。否则的话还要再遍历一次数组，对第1步低消过程中留存下来的多数元素进行计数，验证其频次是否达到要求（如超过n/2）。

证明

该算法其实有一些前提，那就是超过n/2的多数元素只会有一个，可以用反证法来证明，如果存在两个多数元素，x是多数元素数量为m，y是另一个多数元素数量为n，根据定义，m和n都大于n/2是不可能的，与假设矛盾，因此原命题成立。

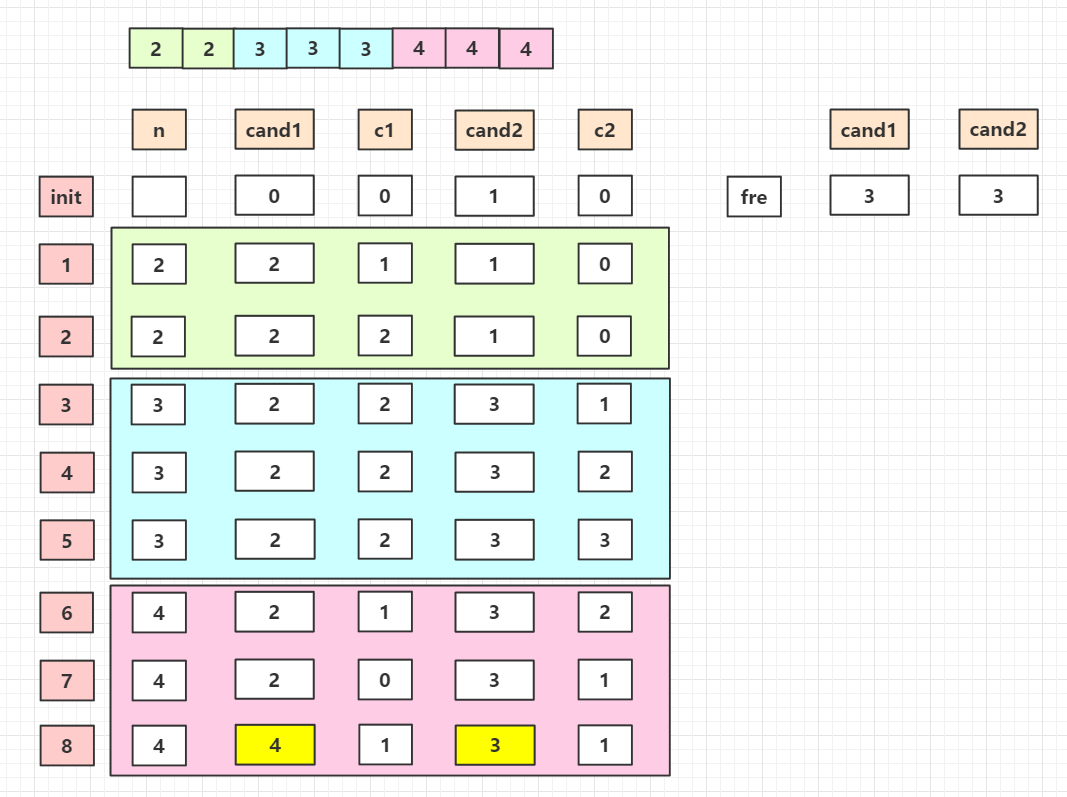
同理，还可以推广到超过n/3的多数最多有2个，超过n/m的多数元素最多有m-1个。

典型题目

典型题目

参考资料

• Boyer-Moore Majority Voting Algorithm
• 图解算法 | 摩尔投票法求多数元素
• 如何理解摩尔投票算法？
• 使用摩尔投票法解决多数问题
• 算法 摩尔投票算法(图解例题)
• 摩尔投票算法( Boyer-Moore Voting Algorithm)
• 摩尔投票法(Boyer–Moore majority vote algorithm)