字符串即由字符组成的线性数组结构，可以理解为字符数组或者字符列表，但元素的集合是有限集合，通常是英文字符，数字和算术运算符号。可以说数组和列表的常见问题和技巧都可以应用于字符串，但因为是有限集合，所以又有一些独特的问题和技巧，今天就来总结一下。

编程技巧

转成字符数组来遍历

对于Java语言来说charAt(i)非常的慢，所以如果需要多次遍历，或者多次获利某个索引位置的字符，最好先转成字符数组toCharArray()，这样效率会高出很多。对于其他语言像Python3和Kotlin则没必要，因为本来就可以像常规数组(列表)一样遍历。

用桶代替哈希表

字符串的每个元素是有限集合，所以要尽可能的用桶来代替哈希表，每当需要对字符计数，或者做映射的时候，都可以先尝试用桶。 比如小写英文字母，就可以用一个长度为26的整数数组来计数，字符与索引的转化关系是ch-‘a’，同理可以扩展到大写ch-‘A’，甚至数字字符ch-‘0’。

字符与索引相互转化

前面提到了用桶，就是把字符转化为索引。反过来也是可行的。目标字符ch = (char) (i + ‘a’)就把索引转为小写，大写和数字字符也是同理的。

Java/C/C++

传统语言里面char相当于无符号整数，所以可以直接强行互转：

1
2

char ch = (char) (i + 'a');
int idx = ch - 'a'

Python3

大Python3中要用ord()和chr()来进行字符到整数的互转

1
2

idx = ord(ch) - ord('a')
ch = chr(idx + ord('a'))

Kotlin

因为Kotlin中没有所谓的基础类型，都是对象，所以就用对象提供的方法即可。字符转为整数用Char.code，要把数字字符转为对应字面的整数用Char.digitToInt，如:

1
2
3

val ch: Char = '3'
println("ch as int ${ch.code}, ch digit as int ${ch.digitToInt()}")
// ch as int 51, ch digit as int 3

如果是想转成其他进制的整数，可以传入基数作为参数，如：

1
2

val hexCh = 'F'
println("hex ch ${hexCh.digitToInt(16)}") // 15

因为是基于JVM的，所以字符也可以用于计算，比如idx = ch - ‘a’，这是完全没有问题的。

1
2
3
4
5

val a = 'a'
var idx = 'd' - a
val aidx = idx + 7
println("idx $idx, aidx to ch ${(aidx + 'a'.code).toChar()}")
//idx 3, aidx to ch k

反过来，整数转到字符，用Int.toChar()就可以了，会按ASCII的code值去转。另外，如果想转成数字字符用Character.forDigit(ch, radix):

1
2

val d = 8
println(" int to char ${d.toChar()}, to digit char ${Character.forDigit(d, 10)}")

字符数组/列表转为String

涉及字符的题目，一般需要转成字符数组处理后，再把字符数组转成字符串。

对于Java来说，String的构造方法支持传入char[]作为参数。

而Python3，其实就是字符列表转为字串，可以用join方法，这个方法是str提供的方法，用一个str当作分隔符来把一个列表连接起来：

1
2

chars = ['H', 'e', 'l', 'l', 'o']
''.join(chars) # "Hello"

同样，Kotlin中也有joinToString方法，它对数组和列表都支持，可以传入一个参数作为分隔符：

1
2

val chars = charArrayOf('H', 'e', 'l', 'l', 'o')
val res = chars.joinToString("")

压缩到位运算

如果字符集合特别有限，比如只有有限几个字符，或者只有小写，只有大写，这时可以更进一步的，用位运算来进行优化。小写字符只有26个，一个整数有32位可以用，完全够用。

当满足以下两个条件时就可以考虑用位运算来优化：仅涉及两个状态，有和没有；另外就是字符或者组合后的集合范围在32个以内。

典型问题

变位词

变位词是指对于一个字符串，把某几个字符位置换一下之后得到的字符串，与原串互为变位词。其实变位词不局限于字符串，对于任何一个线性列表来说，把某几个元素位置变一下就是互为变位词了。变位词有两大特点：字符集合是一样的，种类一样，频次也一样，但排列不一样。

基于它的特点，涉及变位词的问题，就变成了字符频次统计的问题了，如果两个字符串的字符频次一样，那么就互为变位词。另外的处理方式就是排序，因为只是排列不一样，所以按照同一规则排序后，两字符串就相同了，那么通过排序 来验证也可以可行的。具体处理时，要依据不同的条件来灵活选择具体的识别方式。

需要注意的是，当用频次统计法时，记得用桶而不是直接用哈希表。

典型问题

回文

典型问题

状态压缩

典型问题

有限状态自动机DFA

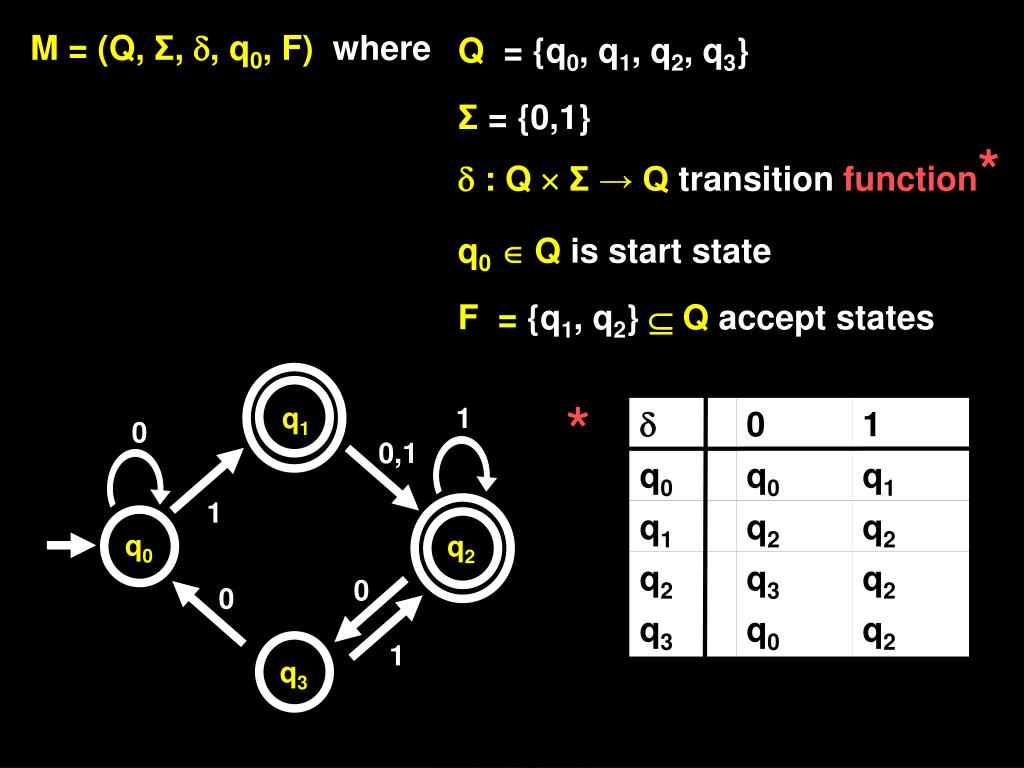
DFA就是状态机，每次读入一个字符，根据当前状态和字符进行状态转移，它可以解决『对于给定的输入字符串S，判定其是否滞条件P』之类的问题。但是一种非常优雅的方式，而不是到处是if-else判断。

注意：准确的来说，DFA的输入是一个『序列』，就是说每个元素都是按顺序的一次一个的被DFA读入，并不会停滞，跳过或者回溯，当然了字符串是最常见的一种序列，我们从前往后的依次读入每个字符。状态机的最大优势在于它把逻辑和规则进行抽象，变成了状态和状态转移，从而大大简化了逻辑。如果不用状态机，逻辑会很混乱，并且也会用一些零散的变量来代表状态，对于简单的题目可能还好，比如LeetCode #8，但像LeetCode #65，当状态比较多时，状态机的优势就会非常的明显，如果不用状态机，依然要用很多变量来表示，比如有没有e/E，有没有小数点，小数点左右有没有数字？但如果能抽象出状态，那么这些都是状态机中的一个状态，整体逻辑会简化不少。

应用DFA的步骤：1）厘清出规则，也就是要把S以怎么一种条件进行约束，会得到两种数据，一个是状态，一个是字符集合；2）定义状态，一个状态就是 条件约束下的一个合法的部分；3）找出字符集合，也就是条件限制出的特定的字符集合。

以LeetCode #8为例，状态可以定义为：

• STARTED 开始状态，初始状态
• SIGNED 符号态，遇到了符号就转入了符号态
• IN_NUMBER 数字态
• ENDED 终止状态

字符集合，也就是：

• 空格，连续的前导空格
• 符号，+或者-
• 数字，数字字符0~9
• 其他字符，非以上三种的其他字符

明确了，状态和字符集合，就可以依据规则写出状态转移表格了，而有了状态转移就可以写出代码了，具体的可以参看具体问题的题解。

典型问题

参考资料

• 自动机
• 有穷自动机DFA&NFA (学习笔记)
• Deterministic Finite Automaton
• Deterministic Finite Automata
• Introduction of Finite Automata
• Deterministic Finite Automaton

其他

典型问题