稀有猿诉

十年磨一剑，历炼出锋芒，说话千百句，不如码二行。

前缀和与差分数组简介

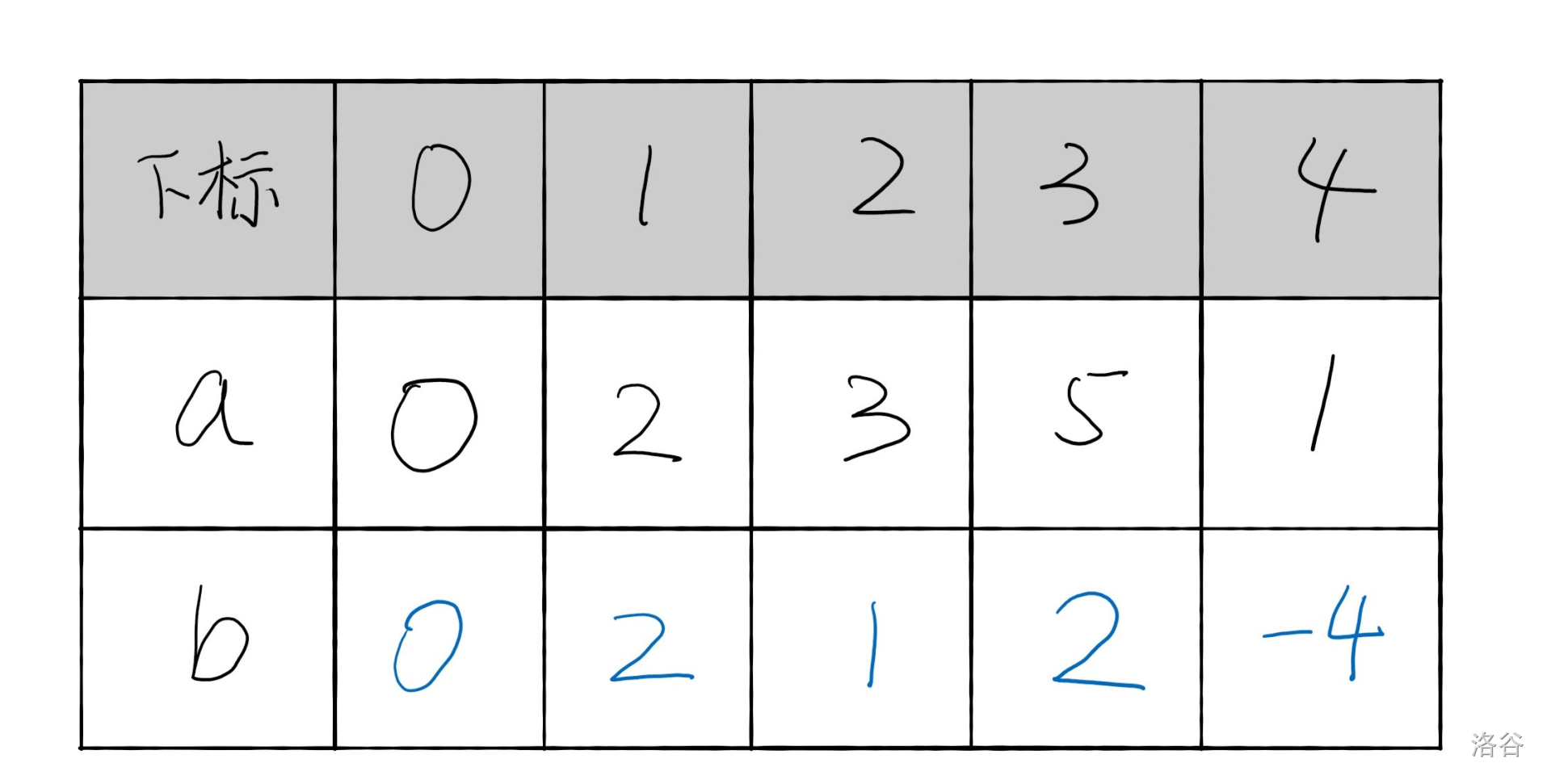
在数组相关的问题中前缀和与差分数组是使用使用比较多的辅助数组，能有效的提升效率。前缀和就是数组中到当前元素的和；差分数组是一个辅助数组，每个元素是原数组相邻元素之差，故命名为差分数组，它在原数组区间修改等操作上能辅助提升效率。

一维前缀和

前缀和的定义不复杂，对于一维列表来说，前缀和是一个辅助列表，前缀和中的元素i，就是原列表中从元素0到元素i的累加和，即preSum[i] = sum(nums, 0, i)。

1
2
3
4

preSum[0] = nums[0]
preSum[1] = nums[0] + nums[1] = preSum[0] + nums[1]
preSum[2] = nums[0] + nums[1] + nums[2] = preSum[1] + nums[2]
preSum[n-1]= nums[0] + nums[1] + ... + nums[n - 1] = preSum[n - 2] + nums[n - 1]

代码实现就是这个样的：

1
2
3
4
5
6
7
8
9
10

private void init() {
    if (size < 1) {
        return;
    }
    preSum[0] = nums[0];

    for (int i = 1; i < size; i++) {
        preSum[i] = preSum[i - 1] + nums[i];
    }
}

前缀和的应用

前缀和最大的作用就是能够以常数时间求出一维列表的区间和，或者说连续子列表的和。

比如给定一个列表nums，长度是n，如果想求出子列表[l, r]，都是闭区间的子列表的和，就可以用前缀和。朴素做法很容易想到，就是从遍历区间[l, r]累加即可，显然这是O(n)复杂度，如果查询就一次两次的，当然 也可以，但如果查询次数多了，显然效率差，如果查询m次，时间复杂度会上升到O(mn)。

区间和[l, r]，记为sum(l, r) = nums[l] + nums[l + 1] + … + nums[r-1] + nums[r]，是可以转化用前缀和来求解的，过程如下：

1
2
3

sum(l, r) = nums[l] + nums[l + 1] + ... + nums[r-1] + nums[r]
           = nums[0] + nums[1] +... + nums[l-1] + nums[l] + ... nums[r-1] + nums[r] - (nums[0] + nums[1] +...+ nums[l-1])
           = preSum[r] - preSum[l-1]

事先计算前缀和列表，就可以直接以一次减法求出区间和：

1
2
3
4
5
6

private int regionSum(int i, int j) {
    if (i == 0) {
        return preSum[j];
    }
    return preSum[j] - preSum[i - 1];
}

完整代码看这里。

前缀和典型题目

题目 题解 说明
560. 和为 K 的子数组 题解
813. 最大平均值和的分组 题解
1732. 找到最高海拔 题解
2559. 统计范围内的元音字符串数 题解
题解
题解
题解

差分数组

与前缀和类似，差分数组也是一个常用的辅助数组。它的定义是原数组相邻两元素之差：

1
2
3
4
5

diff[i] = nums[i] - nums[i - 1]
diff[0] = nums[0]
diff[1] = nums[1] - nums[0]
diff[2] = nums[2] - nums[1]
diff[n-1] = nums[n-1] - nums[n-2]

不难发现，差分数组是前缀和的逆运算，也就是说把差分数组diff求它的前缀和，刚好能得到原始数组：

1
2
3
4

nums[0] = diff[0]
nums[1] = nums[0] + nums[1] - nums[0] = diff[0] + diff[1]
nums[2] = nums[0] + nums[1] - nums[0] + nums[2] - nums[1] = diff[0] + diff[1] + diff[2]
nums[n-1] = nums[0] + nums[1] - nums[0] + ... nums[n-1] - nums[n-2] = diff[0] + ... diff[n-1]

差分数组的作用

差分数组的作用是能快速的对区间更新。区间更新是指对于数组nums，长度为n，想要对区间[l, r]做更新，比如都加上一个数x，或者都减去一个数y。常规的实现肯定遍历[l, r]然后对每个元素做更新，这是线性时间O(n)的，而用差分数组可以在常数时间完成区间更新。

1
2
3

nums[l, r] + x = nums[l] + x, nums[l + 1] + x, ... nums[r-1] + x, nums[r] + x
                  = diff[l] + x, diff[l + 1], .... diff[r-1], diff[r], diff[r + 1] - x
                  = diff[l] + x, diff[r+1] - x

可以看出，只对差分数组的区间两端做加减法就可以实现原数组区间增加。当然了，如果想得出原数组的真实修改后的结果，仍需要对差分数组做前缀和才可以，因为差分数组的前缀和才是原始数组。所以，差分数组是一个辅助数组，它的作用不像前缀和那样明显，它只能配合使用，无法单独使用。（单独使用仍要用O(n)来计算前缀和才能得到原始数组，失去了意义）。

差分数组与前缀和通常作为辅助数组一起使用，以解决快速区间查询和区间修改，这便是树状数组，理解 了前缀和和差分数组的作用，对于理解 树状数组有很大的帮助。树状数组的具体原理与应用可以参考 这篇文章。

差分典型题目

题目 题解 说明
2303. 计算应缴税款总额 题解
题解
题解

拓展到二维

一维上能做的事情，肯定 都能拓展到二维，对于二维列表也就是说矩阵，也可以使用前缀和和差分，差分本来的应用比较有限，不像前缀和可以单独应用，并且二维差分要复杂的多得多，所以这里就讨论一下二维前缀和。

假设一个矩阵为matrix，尺寸是mxn，即m行n列，对于它的任意一个格子{i, j}和前缀和preSum[i, j]等于其左上部分的所有元素之和。

1
2
3
4
5

preSum[0, 0] = matrix[0, 0]
preSum[0, 1] = matrix[0, 0] + matrix[0,1] = preSum[0, 0] + matrix[0, 1]
preSum[1, 0] = matrix[0, 0] + matrix[1, 0] = preSum[0, 0] + matrix[1, 0]
preSum[1, 1] = matrix[0,0] + matrix[0,1] + matrix[1,0] + matrix[1,1] = preSum[0, 1] + preSum[1, 0] + nums[1,1] - preSum[0,0]
preSum[i, j] = preSum[i-1,j] + preSum[i, j-1] + matrix[i,j] - preSum[i-1,j-1]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

private void init() {
    preSum = new int[m][n];

    if (m < 1 || n < 1) {
        return;
    }

    preSum[0][0] = matrix[0][0];
    preSum[1][0] = preSum[0][0] + matrix[1][0];
    preSum[0][1] = preSum[0][0] + matrix[0][1];

    for (int i = 1; i < m; i++) {
        for (int j = 1; j < n; j++) {
            preSum[i][j] = preSum[i][j - 1] + preSum[i - 1][j] + matrix[i][j] - preSum[i - 1][j - 1];
        }
    }
}

二维前缀和的应用

与一维前缀和类似，二维前缀和的应用用于快速求出区间和，比如求子矩阵和，求[r1,c1]到[r2,c2]之间的子矩阵之和，就可以应用二维前缀和，可以从O(mn)的复杂度降到O(1)。

1

sum[r1,c1]~[r2,c2] = preSum[r2,c2] - preSum[r2,c1-1] - preSum[r1-1, c2] + preSum[r1-1, c1-1]

1
2
3
4
5
6

public int regionSum(int r1, int c1, int r2, int c2) {
    if (r1 == 0 && c1 == 0) {
        return preSum[r2][c2];
    }
    return preSum[r2][c2] - preSum[r2][c1 - 1] - preSum[r1 - 1][c2] + preSum[r1 - 1][c1 - 1];
}

两个坐标[r1,c1]和[r2,c2]把矩阵分成了三个区域，一是[0, 0]~[r2,c2]这就是preSum[r2,c2]，二是[0,0]~[r2,c1-1]，三是[0,0]~[r1-1,c2]，相减，多减了一个公共区域[0,0]~[r1-1,c1-1]，所以要加回来。

完整代码看这里。

前缀和与差分数组一般作为辅助数组使用，理解了它们的原理对于理解更复杂的数组结构如树状数组是非常有帮助的，关于树状数组可以参考 此文。

典型问题

题目 题解 说明
304. 二维区域和检索 - 矩阵不可变 题解 二维前缀和
1314. 矩阵区域和 题解

拓展到后缀和最值

前缀和是最常用的一种前缀辅助数组，但并不局限于此，也可以用后缀和，视具体情况而定。

另外，还可以拓展到最值，就是说前缀最值（最小值最大值），或者后缀最小值最大值，也可以帮助降低复杂度。

典型问题

题目 题解 说明
238. 除自身以外数组的乘积 题解 前缀乘积，后缀乘积
731. 我的日程安排表 II 题解 TreeMap当作差分数组
775. 全局倒置与局部倒置 题解 后缀最小值
915. 分割数组 题解 后缀最小值辅助数组
题解
题解

参考资料

Comments